2D Radial Ramp 구현: 두 가지 접근 방식
2D 공간에서의 Radial Ramp는 이미지를 기준으로 중심에서 바깥쪽으로 점진적으로 변화하는 값을 계산하는 작업입니다. 이 작업은 주로 비네팅 효과(vignetting), 마스크 생성, 혹은 기타 그래픽적 효과를 구현할 때 유용합니다. 이 섹션에서는 두 가지 방식으로 Radial Ramp를 구현하는 방법을 살펴보고, 각각의 핵심 아이디어와 과정을 정리하겠습니다.
1. 첫 번째 접근 방식: 거리 공식 기반
개요
첫 번째 방법은 간단한 거리 공식(distance formula)을 기반으로 하여 각 픽셀의 중심으로부터의 거리를 계산하고 이를 Normalize(정규화)하여 Ramp를 생성합니다.
주요 공식
거리 공식:

이를 이용해 중심에서 바깥으로 갈수록 값이 증가하는 Radial Ramp를 생성할 수 있습니다.
코드 분석
kernel Radial : ImageComputationKernel<ePixelWise>
{
Image<eRead,eAccessRandom,eEdgeClamped> src; // 입력 이미지
Image<eWrite> dst; // 출력 이미지
param:
float mult; // 확대 배율
local:
float cx; // 중심 X 좌표
float cy; // 중심 Y 좌표
float xt; // 이미지 폭
float yt; // 이미지 높이
void define(){
defineParam(mult, "mult", 1.0f); // mult 기본값 설정
}
void init(int2 pos){
xt = src.bounds.x2; // 이미지 폭
yt = src.bounds.y2; // 이미지 높이
cx = xt / 2.0f; // 중심 X 계산
cy = yt / 2.0f; // 중심 Y 계산
}
void process(int2 pos){
// 픽셀의 중심으로부터의 거리 계산 및 정규화
dst() = sqrt(pow((pos.x - cx) / (xt / mult), 2) +
pow((pos.y - cy) / (yt / mult), 2));
}
};주요 과정
- 파라미터 정의:
mult: 거리 값을 확대/축소할 배율을 설정.
- 초기화 (init):
- 이미지의 폭(
xt)과 높이(yt)를 계산. - 이미지의 중심 좌표(
cx,cy)를 계산.
- 이미지의 폭(
- 프로세스 (process):
- 각 픽셀의 좌표를 중심 좌표(
cx,cy)와 비교하여 상대적 거리 계산. sqrt와pow를 사용하여 거리 값 생성.- 거리 값에
mult를 적용해 스케일링.
- 각 픽셀의 좌표를 중심 좌표(

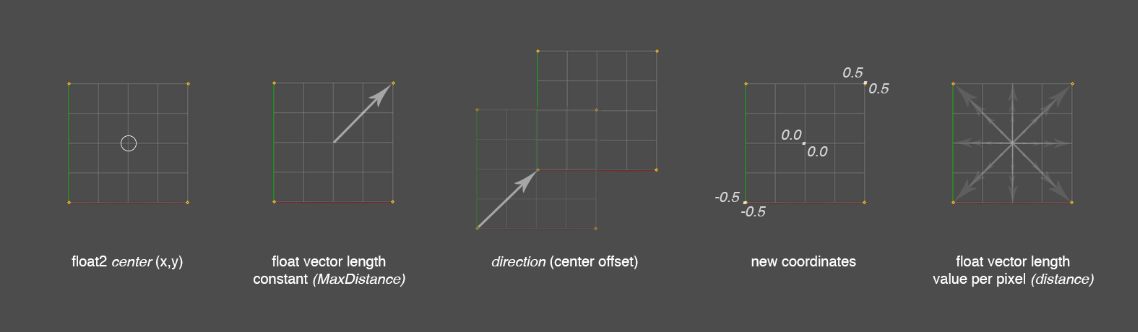
2. 두 번째 접근 방식: 벡터 길이와 노멀라이즈 사용
개요
두 번째 방법은 벡터 연산과 벡터 길이(length)를 활용하여 Radial Ramp를 생성합니다. 이 방법은 벡터의 방향성과 길이를 계산하며, 중심으로부터의 상대적 거리를 간단하게 표현할 수 있습니다.
주요 공식
벡터 길이 공식:

노멀라이즈된 거리:

여기서 MaxDist는 중심에서 이미지 가장자리(코너)까지의 최대 거리입니다.
코드 분석
kernel Radial_2 : ImageComputationKernel<ePixelWise>
{
Image<eRead,eAccessRandom,eEdgeClamped> src; // 입력 이미지
Image<eWrite> dst; // 출력 이미지
param:
float gamma; // 감마 파라미터
bool invert; // 반전 여부 설정
local:
float xt; // 이미지 너비
float yt; // 이미지 높이
float2 position; // UV 좌표
float2 direction; // 정규화된 UV 좌표
float2 center; // 이미지의 중심
float distance; // 중심에서부터의 거리
float MaxDist; // 중심에서 이미지 경계까지의 최대 거리
float distanceNorm; // 정규화된 거리
float out;
void define(){
defineParam(gamma,"gamma",1.0f); // 감마 기본값 설정
defineParam(invert,"invert", false); // 반전 기본값 설정
}
void init(int2 pos){
xt = src.bounds.x2; // 이미지의 가로 경계값
yt = src.bounds.y2; // 이미지의 세로 경계값
center = float2(xt/2 , yt/2); // 이미지 중심을 float2로 정의
MaxDist = length(center); // 중심에서 경계까지의 벡터 길이 계산
}
void process(int2 pos){
float2 position = float2 (pos.x, pos.y); // 각 픽셀의 X와 Y 좌표
float2 direction = position - center; // 중심을 기준으로 한 위치 오프셋
float distance = length(direction); // 각 픽셀이 중심에서 떨어진 거리 계산
float distanceNorm = distance / MaxDist; // 정규화된 거리 계산
float out = invert == true ? distanceNorm : 1.0f / distance; // 반전 조건에 따라 출력값 설정
dst() = pow(out,gamma); // 감마 값을 적용하여 최종 출력
}
};주요 과정
- 파라미터 정의:
gamma: 감마 보정을 위한 파라미터.invert: Radial Ramp를 반전할지 결정하는 Boolean 값.
- 초기화 (init):
- 이미지의 폭(
xt)과 높이(yt)를 계산. - 중심 좌표(
center)를float2로 계산. - 중심에서 가장자리까지의 최대 거리(
MaxDist)를 계산.
- 이미지의 폭(
- 프로세스 (process):
- 픽셀 좌표를
float2로 변환. - 픽셀과 중심 간의 벡터 계산(
direction). - 벡터의 길이(
length)를 이용해 거리 계산. - 정규화된 거리(
distanceNorm) 또는 반전된 거리(1.0f / distance) 계산. - 감마 보정(
pow) 적용 후 출력.
- 픽셀 좌표를

두 방법의 비교
| 항목 | 첫 번째 방법 | 두 번째 방법 |
| 기술적 복잡도 | 간단, 거리 공식을 직접 사용 | 벡터 연산과 정규화를 사용 |
| 유연성 | 적은 파라미터로 단순 계산 수행 | 추가 파라미터(gamma, invert)로 조정 가능 |
| 효율성 | 상대적으로 빠름 | 약간 더 복잡하지만 유용한 벡터 개념 도입 |
| 활용성 | 간단한 효과(비네팅 등)에 적합 | 다양한 그래픽 효과 구현 가능 |
결론
두 가지 방법 모두 Radial Ramp를 효과적으로 구현할 수 있지만, 벡터 기반 방법은 더 유연하며 다양한 그래픽 효과에 응용될 수 있습니다. 반면, 첫 번째 방법은 간단한 구현과 빠른 계산이 필요할 때 유용합니다.
이 두 접근법을 이해하고 활용하면, 복잡한 그래픽 효과나 이미지 프로세싱 작업에서 더욱 창의적이고 강력한 솔루션을 개발할 수 있습니다.
'Nuke > Blink Script' 카테고리의 다른 글
| Blink Scripting 101 - C++의 For 루프 (0) | 2024.12.11 |
|---|---|
| Blink Scripting 101 - 이미지 변환 적용 (0) | 2024.12.11 |
| Blink Scripting 101 - UV 맵 생성 예제 (0) | 2024.12.11 |
| Blink Scripting 101 - Combining Input Image and Custom Color (0) | 2024.12.11 |
| Blink Scripting 101 - Custom_Color (0) | 2024.12.11 |


