이미지 변환 적용: 이분선형 보간법, 스케일링, 회전
제공된 코드는 이분선형 보간법, 스케일링, 회전과 같은 다양한 이미지를 변환하는 기술을 보여줍니다. 이 변환들은 이미지의 각 채널(RGBA)을 개별적으로 제어할 수 있으며, 이미지를 다루는 방식에 대한 유연성을 제공합니다. 아래는 코드에서 설명된 주요 개념과 구현 내용을 정리한 것입니다.
이분선형 보간법 (Bilinear Interpolation)
이분선형 보간법은 픽셀 좌표 사이의 부동소수점 위치에 대해 픽셀 값을 보간하는 방법입니다. 이 방법은 대상 좌표와 주변 픽셀 그리드 사이의 비율을 기반으로 주변 픽셀 값의 가중 평균을 계산합니다.
기본 이분선형 변환
기본 변환 코드는 이분선형 보간법을 적용하여 이미지를 이동시키는 작업을 합니다. 이동은 X, Y 축에 대한 오프셋 값에 따라 결정됩니다. 이 오프셋은 이미지 내에서 이미지를 이동시키는 역할을 합니다.
kernel Transform : ImageComputationKernel<ePixelWise>
{
Image<eRead,eAccessRandom,eEdgeClamped> src; // 입력 이미지
Image<eWrite> dst; // 출력 이미지
param:
float2 Offset; // 오프셋 파라미터
void define(){
defineParam(Offset, "Position", float2(128.0f, 128.0f)); // 기본 오프셋 값 설정
}
void process(int2 pos){
// 이분선형 보간법을 적용하여 픽셀을 이동
dst() = bilinear(src, pos.x - (Offset.x - 128), pos.y - (Offset.y - 128));
}
};
위 코드에서는 Offset 값을 사용하여 이미지의 각 픽셀을 이동시키는 방식입니다. Offset 값에 따라 이미지를 번역하거나 변환할 수 있습니다.

채널별 이분선형 보간법
이미지의 각 채널(R, G, B)을 개별적으로 제어할 수 있는 코드를 작성할 수도 있습니다. 이를 통해 각 채널에 다른 오프셋 값을 적용하고, 채널별로 변환을 다르게 할 수 있습니다.
kernel TransformRGB : ImageComputationKernel<ePixelWise>
{
Image<eRead,eAccessRandom,eEdgeClamped> src; // 입력 이미지
Image<eWrite> dst; // 출력 이미지
param:
float2 OffsetRed; // 빨간색 채널 오프셋
float2 OffsetGreen; // 초록색 채널 오프셋
float2 OffsetBlue; // 파란색 채널 오프셋
void define(){
defineParam(OffsetRed, "Position Red", float2(128.0f, 128.0f)); // 빨간색 채널 기본값
defineParam(OffsetGreen, "Position Green", float2(128.0f, 128.0f)); // 초록색 채널 기본값
defineParam(OffsetBlue, "Position Blue", float2(128.0f, 128.0f)); // 파란색 채널 기본값
}
void process(int2 pos){
dst(0) = bilinear(src, pos.x - (OffsetRed.x - 128), pos.y - (OffsetRed.y - 128), 0); // 빨간색 채널
dst(1) = bilinear(src, pos.x - (OffsetGreen.x - 128), pos.y - (OffsetGreen.y - 128), 1); // 초록색 채널
dst(2) = bilinear(src, pos.x - (OffsetBlue.x - 128), pos.y - (OffsetBlue.y - 128), 2); // 파란색 채널
dst(3) = 1.0f; // 알파 채널
}
};
이 코드에서는 각 채널에 대해 별도의 오프셋을 적용하여, 채널별로 다른 이동을 할 수 있도록 설정하였습니다. 이렇게 하면 각 채널에 대해 독립적인 변환을 할 수 있어 이미지의 세부적인 변형을 가능하게 합니다.

스케일링
스케일링은 이미지를 크기 변화시키는 방법입니다. 기본적으로는 크기를 일정 비율로 늘리거나 줄이는 방식입니다.
기본 스케일링
스케일링을 구현하는 코드는 이미지의 픽셀 좌표를 스케일 인자에 따라 나누어 줍니다. 이를 통해 이미지를 축소하거나 확대할 수 있습니다.
kernel Scale : ImageComputationKernel<ePixelWise>
{
Image<eRead,eAccessRandom,eEdgeClamped> src; // 입력 이미지
Image<eWrite> dst; // 출력 이미지
param:
float Scale; // 스케일 파라미터
void define(){
defineParam(Scale, "Scale", 1.0f); // 기본 스케일 값 1.0f
}
void process(int2 pos){
// 이분선형 보간법을 적용하여 스케일링
dst() = bilinear(src, pos.x / Scale, pos.y / Scale);
}
};
이 코드는 Scale 값에 따라 이미지를 축소하거나 확대합니다. Scale 값을 1.0으로 설정하면 원본 크기 그대로 유지되고, 그보다 작거나 큰 값으로 설정하면 이미지 크기가 축소되거나 확대됩니다.

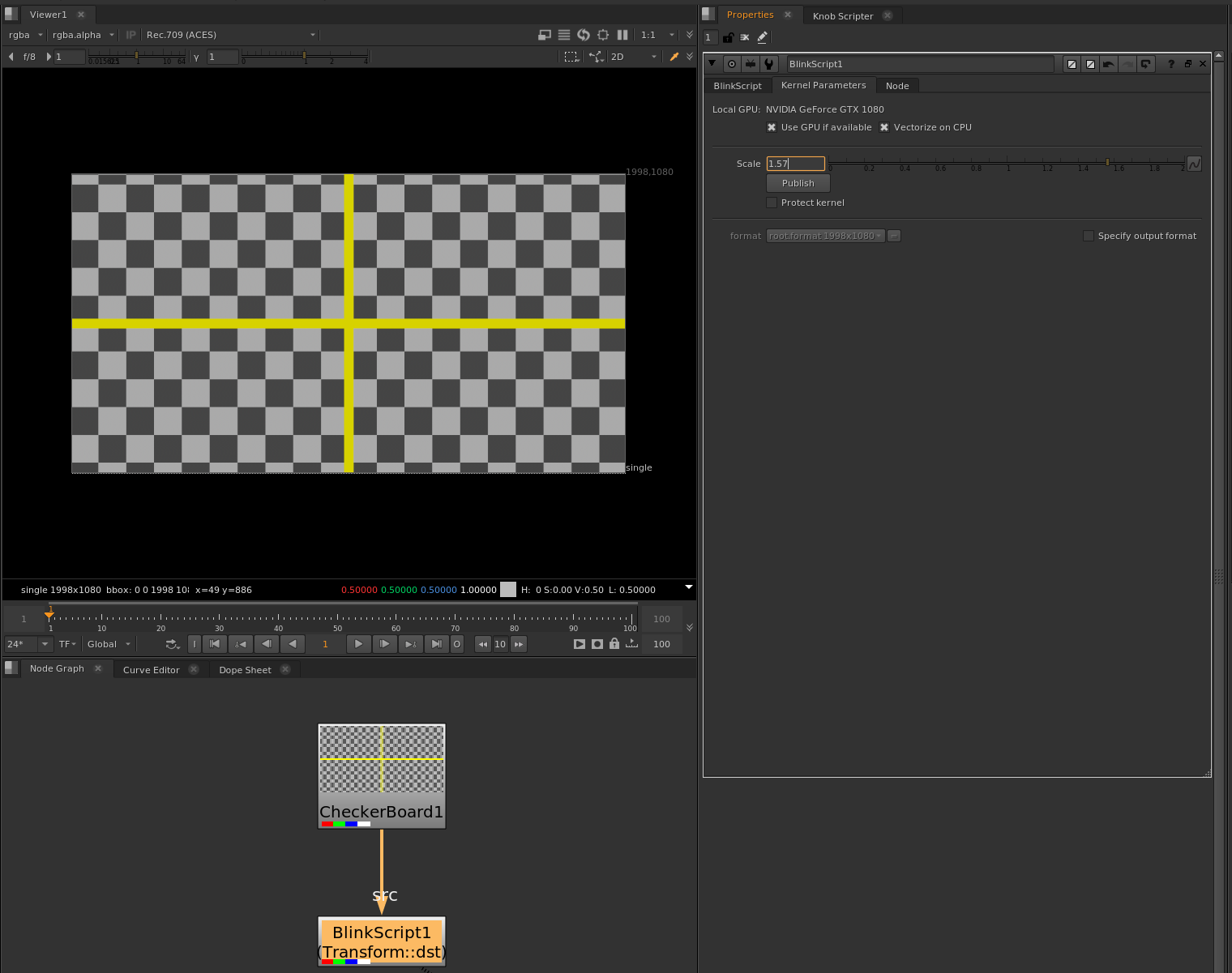
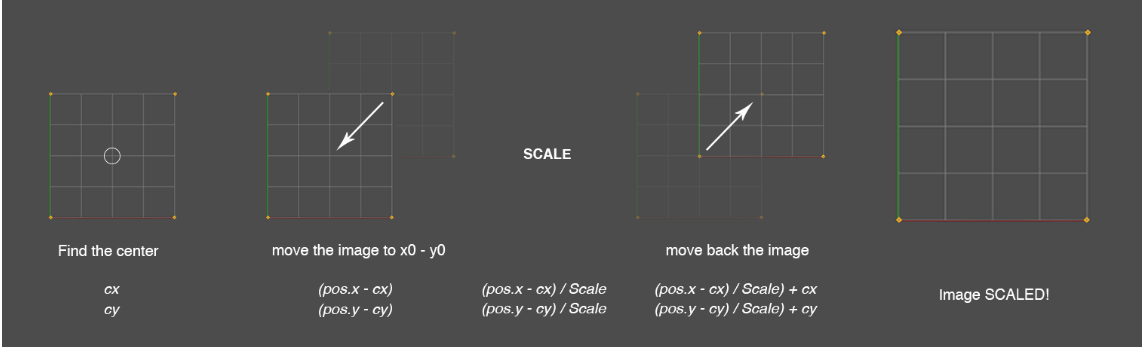
중심으로 스케일링
이미지를 중심으로 스케일링하려면, 스케일링을 수행하기 전에 이미지를 중심으로 이동시키고, 스케일링 후 다시 원래 위치로 되돌리는 과정이 필요합니다.
kernel ScaleCenter : ImageComputationKernel<ePixelWise>
{
Image<eRead,eAccessRandom,eEdgeClamped> src; // 입력 이미지
Image<eWrite> dst; // 출력 이미지
param:
float Scale; // 스케일 파라미터
local:
float cx, cy; // 이미지의 중심 좌표
void define(){
defineParam(Scale, "Scale", 1.0f); // 기본 스케일 값 1.0f
}
void init(int2 pos){
cx = src.bounds.x2 / 2.0f; // 이미지의 X 중심 좌표 계산
cy = src.bounds.y2 / 2.0f; // 이미지의 Y 중심 좌표 계산
}
void process(int2 pos){
// 중심을 기준으로 스케일링
dst() = bilinear(src, ((pos.x - cx) / Scale) + cx, ((pos.y - cy) / Scale) + cy);
}
};
이 코드는 이미지를 중심으로 스케일링합니다. 이미지의 중심을 기준으로 스케일을 조정하여, 이미지를 확대하거나 축소할 수 있습니다.
회전
2D 회전 개념과 구현
2D 공간에서의 회전은 간단한 삼각법을 이용하여 구현할 수 있습니다. 회전을 이해하기 위해선 2차원 좌표계에서의 회전 행렬과 그 작동 원리를 살펴봐야 합니다. 회전은 **중심 좌표(x0, y0)**를 기준으로 각도를 기준으로 이루어지며, 이를 수학적으로 표현하면 다음과 같습니다.
1. 회전 공식
위키백과에서 제공하는 2차원 회전 공식을 간단히 설명하면 다음과 같습니다. 이 공식은 회전 행렬에서 유도됩니다.
https://erwanleroy.com/vector-tools-for-nuke-tutorials-and-math/
X' = X * cos(θ) - Y * sin(θ)
Y' = X * sin(θ) + Y * cos(θ
- X', Y': 회전 후의 좌표
- X, Y: 회전 전의 좌표
- θ: 회전 각도(라디안 단위)
2. 각도에서 라디안으로 변환
위 공식에서 각도는 라디안(Radiant) 단위를 사용합니다. 따라서 일반적인 각도(degree)를 라디안으로 변환해야 합니다. 변환 공식은 다음과 같습니다.
Radiants = Angle * (π / 180)
이 공식은 각도를 라디안으로 변환하여 삼각 함수에서 사용할 수 있도록 합니다.
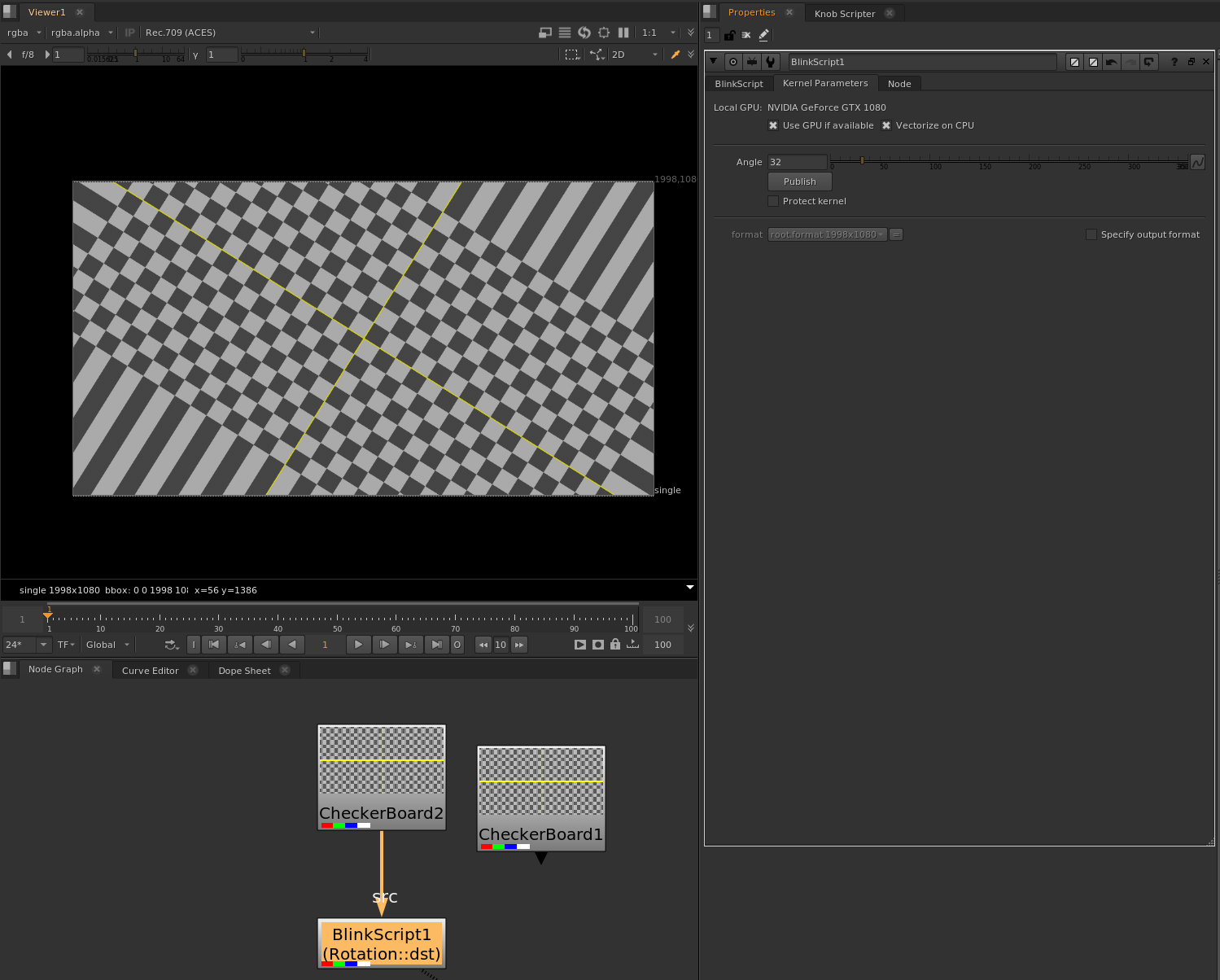
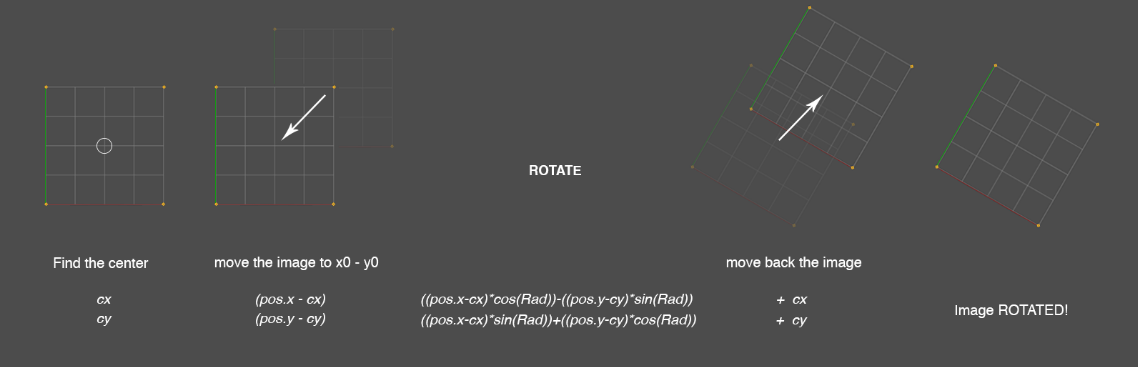
3. 중심 좌표 기반 회전
위 공식의 기본 동작은 좌표의 원점을 기준으로 회전을 수행합니다. 그러나 이미지를 회전할 때는 중심 좌표를 기준으로 회전해야 하므로 다음과 같은 단계를 추가로 수행해야 합니다.
- 기준 좌표 이동: 회전하기 전에 현재 픽셀 좌표를 중심 좌표 기준으로 이동합니다.여기서 cx와 cy는 이미지의 중심 좌표입니다.
- X = pos.x - cx Y = pos.y - cy
- 회전 공식 적용: 이동된 좌표에 대해 회전 공식을 적용합니다.
- X' = X * cos(θ) - Y * sin(θ) Y' = X * sin(θ) + Y * cos(θ)
- 좌표 복구: 다시 원래 좌표계로 복구합니다.
- X_final = X' + cx Y_final = Y' + cy
kernel Rotation : ImageComputationKernel<ePixelWise>
{
Image<eRead,eAccessRandom,eEdgeClamped> src; // 입력 이미지
Image<eWrite> dst; // 출력 이미지
param:
float Angle; // 회전 각도 파라미터
local:
float cx; // 이미지의 가로 중심 좌표
float cy; // 이미지의 세로 중심 좌표
float4 out; // 출력 좌표 벡터
float Radiants; // 라디안 값
float pi; // 원주율 상수 값
void define(){
defineParam(Angle,"Angle",180.0f); // 회전 각도 기본값 설정
}
void init(int2 pos){
cx = src.bounds.x2 / 2.0f; // 이미지의 가로 중심 좌표 계산
cy = src.bounds.y2 / 2.0f; // 이미지의 세로 중심 좌표 계산
pi = 3.14159265359f; // 원주율 상수 값
Radiants = (Angle-180)*(pi/180.0f); // 각도를 라디안 값으로 변환
}
void process(int2 pos){
// 출력 좌표를 회전 (UV 좌표계)
out.x = ( (pos.x-cx) * cos(Radiants) ) - ( (pos.y-cy) * sin(Radiants) ) + cx;
out.y = ( (pos.x-cx) * sin(Radiants) ) + ( (pos.y-cy) * cos(Radiants) ) + cy;
dst(0) = bilinear(src, out.x, out.y,0); // 이분선형 보간법 적용 (R 채널)
dst(1) = bilinear(src, out.x, out.y,1); // 이분선형 보간법 적용 (G 채널)
dst(2) = bilinear(src, out.x, out.y,2); // 이분선형 보간법 적용 (B 채널)
dst(3) = 1.0f; // 알파 채널 값 설정
}
};이 코드는 이미지를 지정된 각도만큼 회전시킵니다. 각도는 Angle 파라미터로 설정하며, 이를 라디안으로 변환하여 회전 공식을 적용합니다.
'Nuke > Blink Script' 카테고리의 다른 글
| Blink Scripting 101 - C++의 For 루프 (0) | 2024.12.11 |
|---|---|
| Blink Scripting 101 - 2D Radial Ramp 구현 (0) | 2024.12.11 |
| Blink Scripting 101 - UV 맵 생성 예제 (0) | 2024.12.11 |
| Blink Scripting 101 - Combining Input Image and Custom Color (0) | 2024.12.11 |
| Blink Scripting 101 - Custom_Color (0) | 2024.12.11 |


